在解釋歐幾里得幾何的基本公設之前,我們先來談談何謂「公設」(Axiom)、以及它存在的理由。
我們都知道,無論說話還是做事,都要有說服得了人的依據。依據決定了我們的言行是否能夠能被人信任。
尤其像是數學這種高度依靠邏輯推理的學術領域,定理和公式就是這種依據。
當我們深入討論數學的本質面向之時,常會有一個問題:「這些定理、公式,是如何推導出來的?」
每一個定理和公式,都可以由更基本的定理所推導而來。底層的定理就像是地基一樣,支撐著它所延伸出來的應用公式,讓數學形成層層相扣的嚴密體系。
若我們不斷地追根溯源,最終會遇到一個問題:「那麼最底層的那些依據,又是從哪裡來的呢?」、「它們是依據什麼而確立的呢?」
所謂的「公設」,就是這種「依據」。它們是不證自明的,當邏輯推理不斷地向回推敲到這個層次,人們通常就不再追問「為什麼它是對的」,而是基於這些公設來建構出整個數學體系。
換言之,當大家接受這些公設時,所有建立於其上而推導出來的所有結論──甚至是一整個體系,都有了穩固的基礎。

接下來簡單講解一下歐幾里得幾何中的五項基本公設:
第一條,任意兩個不同的點之間,都可以劃出一條直線把它們連接起來。
第二條,任意一條直線都可以無限延伸下去。
這句話並不難理解,它的意思是說:雖然現實世界中的直線總會有長度限制,但是在抽象的邏輯世界裡,若將線的兩端持續延長,就可以無窮延伸到看不見盡頭的遠方,而且線還是那麼直。
(請注意,我說的是「抽象的邏輯世界」,現實世界裡我們找不出無限延伸的紙來讓我們畫那種線,也沒人有那種閒工夫。)
第三條,給定一個點作為圓心,任一線段為半徑,就可以畫出一個圓。
只要使用過圓規,相信就不會懷疑這句話的真實性。
第四條,所有直角均為相等。
不會有任何一個直角的角度會大於或小於 90° ,要不然它就不會被稱為「直角」。

第五條公設的情形則相當特別,它的內容是:
若一條直線與另外兩條直線相交,並且在同一側的內角加起來的總和小於 180°,則此兩條直線若無限延伸下去,最終必定會在該側相交。
這條公設又被稱為「平行公設」,用更白話的方式來解釋它的話,意思就是兩條相互平行的線若無限延伸下去,還是會永遠平行,不會在任何一個地方交會。
反過來說,如果兩條線只是肉眼上看起來很平行,但其實我們若多畫條直線與那兩條線相交,所形成的內角並不等於 180° 的話(這就證明了那兩條線其實不平行),若將那兩條線無限地延伸下去,遲早會在遠方的某處相交。
很明顯的,這一條公設在描述和定義上都比其他四條都來得複雜,歷史上關於這條公設的討論和爭議也最多。
「平行公設」本身的敘述過於冗長,因而後世經常使用另一位蘇格蘭數學家:約翰.普萊費爾(John Playfair)所創的「普萊費爾公設」(Playfair's axiom)來加以替代。
給定一條直線、和另一個不在這條線上的點,只能畫出另一條直線能夠通過該點、並與原來那條直線平行。
這五條公設,就是整個歐幾里得幾何的「底層邏輯」,所有的圖形、定理、計算,最終都可以回溯到這些基本原則之上。

通常「公設」的內容都是很直觀的,不需要人們花太多心思來理解。歐幾里得的前四項公設都是如此,很符合我們對於日常世界的理解。
但唯獨那第五條「平行公設」是個例外,光是敘述上就一點也不直觀,還需要另外改寫成「普萊費爾公設」才會比較讓人容易理解。
因此,數學家們一直以來都在懷疑「平行公設」其實並不是一條獨立的公設,可以透過其他更基本的公設推導得出來。歷代以來有許多人曾經試圖證明這一點,但始終徒勞無功。
也有些數學家懷抱著這樣的問題:「如果沒有這條公設,幾何學是否還能成立?」
他們試著捨棄、或是修改平行公設本身的定義,看看是否會產生另一種截然不同的幾何學體系。
這種數學家之中最具代表性的人物,就是俄國的尼可萊.羅巴切夫斯基(Nikolai Lobachevsky)。他對「普萊費爾公設」進行了修改,提出了一個截然不同的假設:
給定一條直線、和另一個不在這條線上的點,可以畫出多條不同的直線通過該點,並且與原來的直線平行。
基於這樣的假設,他從 1829 年開始向學院發表論文,之後逐步推演成另一套邏輯自洽的幾何體系,那就是「雙曲幾何」(Hyperbolic Geometry)。
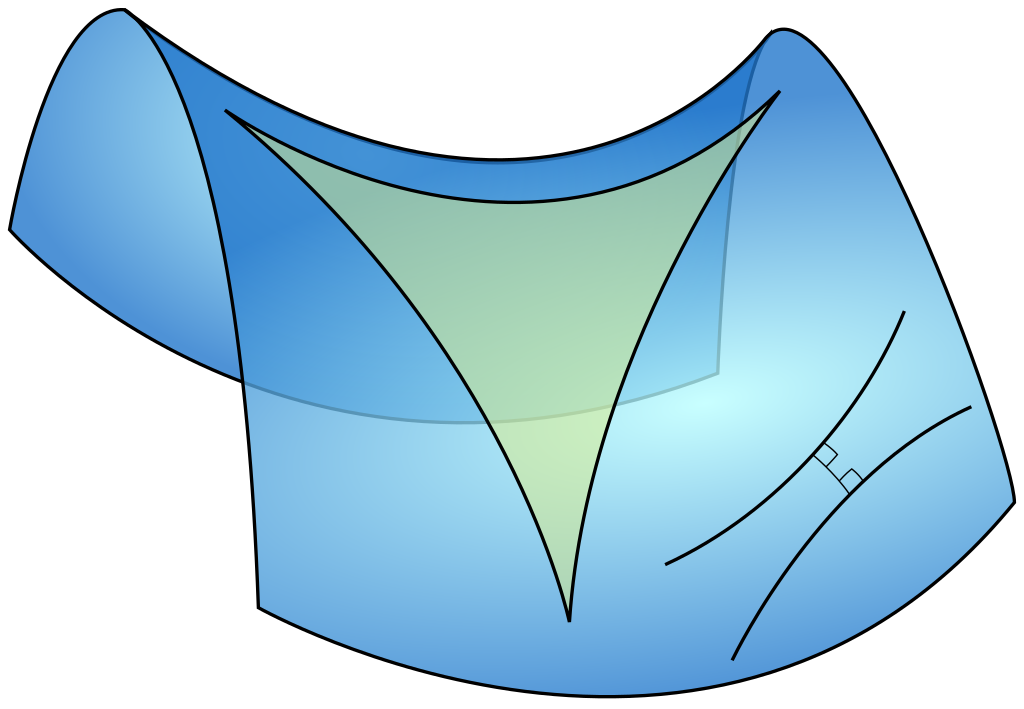
這樣的幾何體系,跟一直以來的歐幾里得幾何有什麼差別呢?簡單來說,歐幾里得幾何所適用的範圍是平面,而雙曲幾何適用的是像下面這種如同馬鞍型狀的曲面空間。
舉一個會讓我們一般人眼睛為之一亮的有趣特性:在雙曲幾何體系裡,三角形的內角總和小於 180° 。這一點相當違反常識,馬上就讓人明白「這的確與我們熟悉的幾何完全不同」。
從此之後,也陸續有其他數學家基於不同版本的「平行公設」,推導出其他適用於曲面空間的幾何體系。這些幾何體系被統稱為「非歐幾何」(Non-Euclidean geometry)。
當愛因斯坦在提出廣義相對論時,也使用到了非歐幾何來描述他理論中的空間形狀。
(以上這張圖簡單展示了「歐幾里得幾何」與「非歐幾何」各自適用的空間類型。)
研究幾何學的發展過程,能讓我們大致了解人類如何建立一個知識體系,以及使用了什麼樣的基本思路。
思路一:建立基礎
歐幾里得的五條公設,定義了我們對於點、線、面等平面空間的基本認識,透過層層推導,從西元前 3 世紀開始就建立起了一整套幾何知識體系。
不只是幾何學或數學,所有的人類知識體系其實都是如此。如果朝向知識的源頭往回推敲,必定可以追溯到一些建構出整個體系的基本核心知識。
從那些核心出發,知識層層地堆疊,建構出我們今日所見的一切。
思路二:將複雜問題拆解成簡單問題
為什麼初步的幾何學裡經常在討論圓形、方形、三角形等簡單形狀,尤其是直角三角形?因為那些是基本中的基本。
任何複雜的幾何圖案或形狀,都可以拆解成以上那些基本形狀和元素。我們可以說整個世界,都是由簡單形狀所組成的。
更重要的是,那些形狀的面積比較容易計算,尤其是直角三角形。也許正因為如此,勾股定理才會在那麼早期的階段就出現在人類歷史之中了吧!
思路三:從有限的已知,推導出重要的未知
人類的認知和能力永遠都會有極限,物理法則本身就是對我們的最大限制。
但人類之所以會發展知識和科技,就是為了盡可能地對抗這樣的極限。
就像是上一篇文章所提到的「三角測量法」這個案例,我們不必直接去量一座山有多高──就算想、我們也做不到,只需要從人類還辦得到的「觀測、測量、推導」開始著手,還是可以用間接的方式,得到我們想知道的資訊。
知識和科技的存在,就是為了滿足這樣的渴望。
思路四:勇於挑戰「基礎」
許多知識體系的基礎公設或原理,都建立在特定的前提和條件。
反過來說,只有當那些前提與條件成立之時,這些公設或原理才有效。也就是說,它們不見得是絕對無法挑戰的「無限上綱」。
有時候,那些前提和條件並非打從一開始就顯而易見的,需要後世的人們投入大量的智慧和研究,不斷地對其發動「挑戰」。
在這個過程之中,有可能花費數個世代的時間,有時也會帶來許多爭論。
爭論或是衝突並不一定是壞事,因為它代表著現有的體系仍有改進的空間,也有可能帶來新的發現與洞見。